Unleashing Transformers: Parallel Token Prediction with Discrete Absorbing Diffusion for Fast High-Resolution Image Generation from Vector-Quantized Codes

arXiv Code Contact Tweet

Summary

We propose a novel parallel token prediction approach for generating Vector-Quantized image representations that allows for significantly faster sampling than autoregressive approaches. During training, tokens are randomly masked in an order-agnostic manner and an unconstrained Transformer learns to predict the original tokens. Our approach is able to generate globally consistent images at resolutions exceeding that of the original training data by applying the network to various locations at once and aggregating outputs, allowing for much larger context regions. Our approach achieves state-of-the-art results in terms of Density and Coverage, and performs competitively on FID whilst offering advantages in terms of both computation and reduced training set requirements.

Samples
Examples of unconditional samples from our models. Our approach uses a discrete diffusion to generate high quality images optionally larger than the training data (right).
Samples
Samples from our models trained on LSUN Churches, FFHQ, and LSUN Bedroom.

Approach

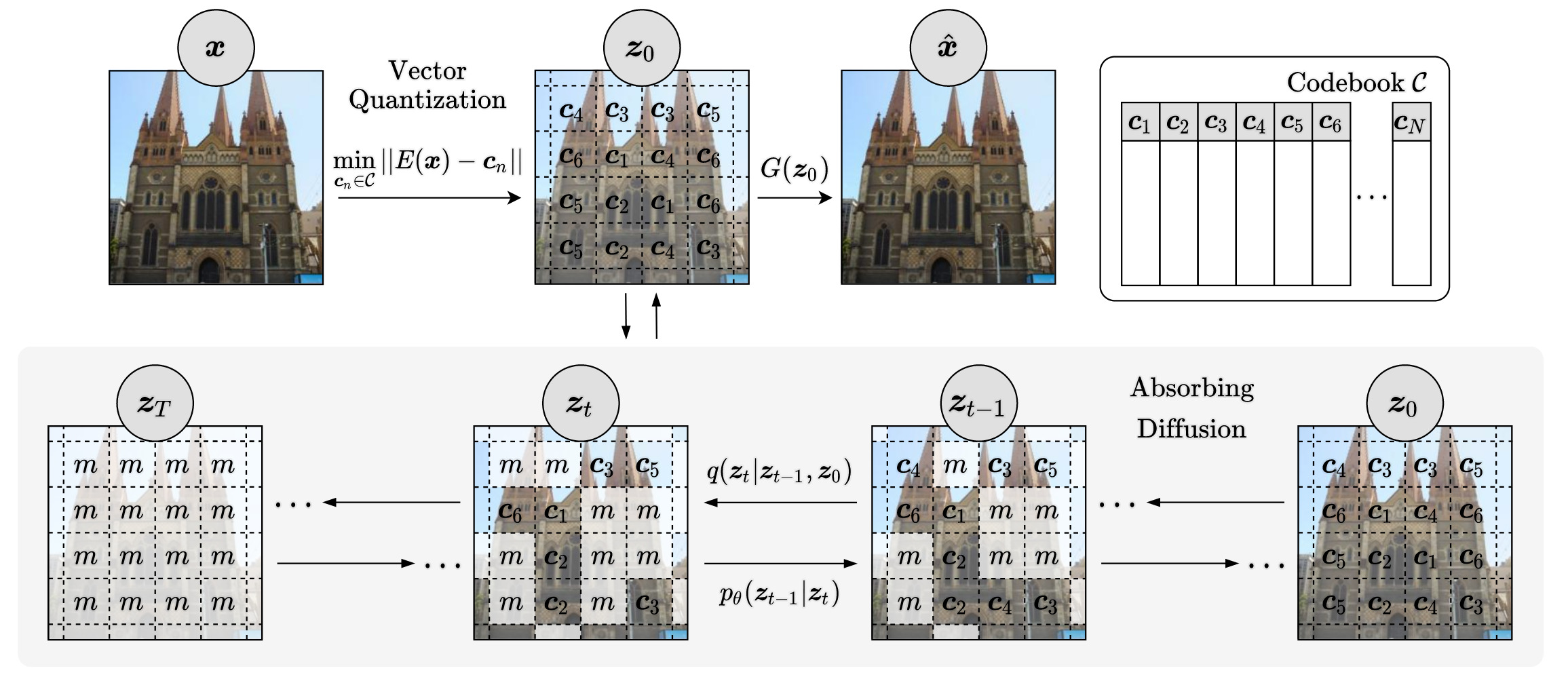
First, a Vector-Quantized image model compresses images to a compact discrete latent space:

\[\boldsymbol{z}_q = q(E(\boldsymbol{x})), \quad \hat{\boldsymbol{x}} = G(\boldsymbol{z}_q),\] \[\text{where } q(\boldsymbol{z}_i) = \underset{\boldsymbol{c}_{j} \in \mathcal{C}}{\operatorname{min}}||\boldsymbol{z}_i - \boldsymbol{c}_j||\]

Subsequently, an absorbing diffusion model learns to model the latent distribution by gradually unmasking latents

\[p_\theta(\boldsymbol{x}_{0:T}) = p_\theta(\boldsymbol{x}_T) \prod_{t=1}^T p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\]

Efficient training is possible by optimising the ELBO,

\[\mathbb{E}_{q(\boldsymbol{z}_0)} \Bigg[ \sum_{t=1}^T \frac{1}{t} \mathbb{E}_{q(\boldsymbol{z}_t|\boldsymbol{z}_0)} \Big[ \sum_{[\boldsymbol{z}_t]_i=m}\log p_\theta([\boldsymbol{z}_0]_i|\boldsymbol{z}_t) \Big] \Bigg]\]

By skipping time steps, sampling can be significantly faster than autoregressive approaches.

Diagram
Our approach uses a discrete absorbing diffusion model to represent Vector-Quantized images allowing fast high-resolution image generation. Specifically, after compressing images to an information-rich discrete space, elements are randomly masked and an unconstrained Transformer is trained to predict the original data, using global context to ensure samples are consistent and high quality.

Evaluation

We evaluate our approach on three high resolution 256x256 datasets, LSUN Churches, LSUN Bedroom, and FFHQ. Below are the quantitative results compared to other approaches. Samples obtained with a temperature value of 1.0 on the LSUN datasets achieves the highest Precision, Density, and Coverage; indicating that the data and sample manifolds have the most overlap. On FFHQ our approach achieves the highest Precision and Recall. Despite using a fraction of the number of parameters compared to other Vector-Quantized image models, our approach achieves substantially lower FID scores.

By predicting tokens in parallel, faster sampling is possible. Specifically, we use a simple step skipping scheme: evenly skipping a constant number of steps to meet some fixed computational budget. As expected, FID increases with fewer sampling steps. However, the increase in FID is minor relative to the improvement in sampling speed.

Table
Quantitative evaluation of our approach on FFHQ, LSUN Bedroom and LSUN Churches. Despite having significantly fewer parameters, our approach achieves lower FID than other Vector-Quantized image modelling approaches.
Big Samples
Examples of samples generated by our model that are larger than those observed in the training data. Global consistency is encouraged by applying the denoising network to all parts of the image and aggregating probabilities.
Random samples from a model trained on LSUN Churches Random samples from a model trained on LSUN Bedroom Random samples from a model trained on FFHQ
Non-cherry picked samples from our models trained on LSUN Churches, LSUN Bedroom, and FFHQ.
Nearest Neighbours in the training data of samples for LSUN Churches Nearest Neighbours in the training data of samples for LSUN Bedroom Nearest Neighbours in the training data of samples for LSUN FFHQ
Nearest neighbours for a model trained on various datasets based on LPIPS distance. The left columns contain samples from our model and the right columns contain the nearest neighbours in the training set (increasing in distance from left to right).
Image inpainting Big Bedrooms Temperature figure
Additional figures from our paper. Left: unlike autoregressive priors, our approach allows internal image regions to edited directly. Middle: unconditional samples from a model trained on LSUN Bedroom larger than images in the training dataset. Right: impact of sampling temperature on diversity, for small temperature changes it is less obvious how bias has changed.